The rules of indices can be found in many calculations, from compound interest to secret codes..
This series of 3 minute math is designed as a quick reminder for some of the main topics, including the rules of indices. I hope they help to provide a focus and a way forward. If you need any more detail please search the site or contact me – always pleased to answer any questions!
All the very best with your studies.
Video Transcript
“Hi and welcome to 3 minute math. In this video we’re talking about ‘the rules of indices’, which some people call ‘powers’ or ‘order’.
Basically, it falls into the BIDMAS order of operations, the ‘I’ stands for indices. There are three main rules you have to remember when dealing with indices, the first is that:
‘a’ to the power of m, multiplied by ‘a’ to the power of ‘n’ is the same as: ‘a’to the power of m add n
This doesn’t really make much sense, but if we put this into a real practical example, things become clearer.
4 to the power of 3, multiplied by 4 to the power of 7 …all you do is add these powers or indices together, giving you 4 to the power of 10.
So which is the answer to this question and the first important rule.
The second rule is:
‘a’ to the power of m, divided by ‘a’ to the power of n is the same as ‘a’ to the power of m minus n
So again, a proper example of this:
six to the power of seven divided by six to the power of two …all you do is subtract the powers, giving you six to the power of five
So,
So, on to the third rule:
(‘a’ to the power of m) note the brackets multiplied to the power of n is…’a’ to the power of m, multiplied by n
A practical example of this:
eight squared, to the power of six which is…eight to the power of two multiplied by six, or eight to the power of twelve
So,
I’m going to give you one final example of an exam question where what you need to do is simplify:
In order to simplify this we need to use some of the rules I’ve discussed:
six to the power of three, multiplied by six to the power of one is going to use the first rule (adding the powers) and becomes:
Next, six to the power of four, divided by six to the power of two, means using the second rule (subtracting the powers) and becomes:
which is 36, and the answer to this question.
I hope that’s been helpful and I look forward to seeing you inside the next three minutes.”
Watch the video on YouTube 3 Minute Math – Indices
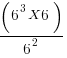
In the last exam style question what would happen if not everything was 6
e.g 6 to the power of 5 times 7 to the power 4, then what would the top
part of the fraction be? +Simon Deacon
how do i graph inequalities
I teach adults, and I email students who missed my sessions links with your
youtube videos. I like your fresh, direct approach, and your explanations
are really clear. Well done. I haven’t had feedback from anybody yet so I
don’t know whether they prefer you or me. The jury’s still out!
i need more advanced than this
ive been taught if you have 6 to the power of 4 x 6 to the power of 0 is 6
to the power of 4 and if you have 3 to the power of 5 x 4 to the power
of 0 its 12 to the power of 6 is this right.
Hi,do you have a video on how to simplify mixed-number fractions? Im 12,
really bad at math and struggle with homework. Your videos help a lot 🙂
Please like and leave a comment!
Visit https://www.3minutemaths.co.uk for real maths, tips and techniques.