Equation of a line
These questions tend to be fairly popular – and are usually presented either as a calculation, or by plotting on a graph yourself. You might also be asked to find some information by reading the graph, or calculate some additional coordinates.
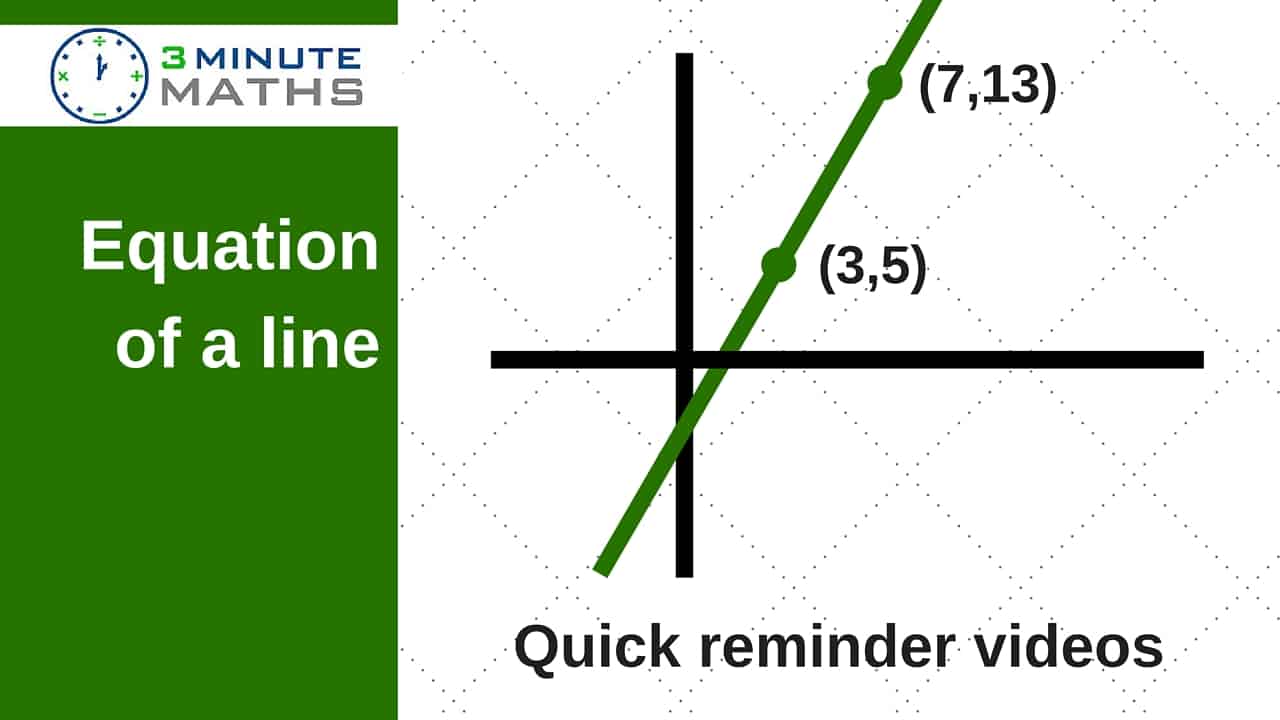
To describe a straight line you only need to know two things –
- How steep it is – the ‘gradient.’ There’s a couple of different ways to present this calculation and I’ve frequently seen something like y2 – y1 / x2 – x1. This is OK but it might be easier to remember ‘diff y / diff x.’
- Where the line started from – the point where it crosses the y axis. This is usually called ‘c’ although some students write this as ‘b.’ There’s no difference 🙂
Whichever way, straight line graphs can be fairly useful and you’ll come across them in many applications such as converting temperature (centigrade to fahrenheit) or distance (miles to kilometres).
Top Tips!
- They follow the general form ‘y = mx + c’
- ‘m’ is the gradient and the easiest way to calculate is difference in y / difference in x
- Gradients that look like a tick are positive
- The other way is negative
- ‘c’ means the point that the line crosses the y axis
- If you don’t know ‘c’ use any set of coordinates to calculate
- You’ll only usually need 3 or 4 points to draw a straight line, on an exam
- The line goes on forever (might be useful to work out some answers)
If you’d like to ask for any more detail, or you’re not sure about anything, please do ask a question in the comments section.
All best with your studies
Watch on YouTube
Straight line graph passing through (1,5) and (2,7) – GCSE maths
Straight line graphs – equation passing through (3,5) and (7,13)
Line with gradient of 6 and passing through (5,10)
Line on a graph – GCSE maths advanced level
[easyazon_image align=”none” height=”160″ identifier=”1447987934″ locale=”UK” src=”https://www.3minutemaths.co.uk/wp-content/uploads/2016/06/51yMr2Q1AvL.SL160.jpg” tag=”matwra-21″ width=”113″]
[easyazon_image align=”none” height=”160″ identifier=”1910602132″ locale=”UK” src=”https://www.3minutemaths.co.uk/wp-content/uploads/2016/06/4128o11qTYL.SL160-1.jpg” tag=”matwra-21″ width=”108″]
[easyazon_image align=”none” height=”160″ identifier=”1844198049″ locale=”UK” src=”https://www.3minutemaths.co.uk/wp-content/uploads/2016/06/51D0Sa98XHL.SL160-1.jpg” tag=”matwra-21″ width=”113″]
Here’s some handwritten notes that might be useful:
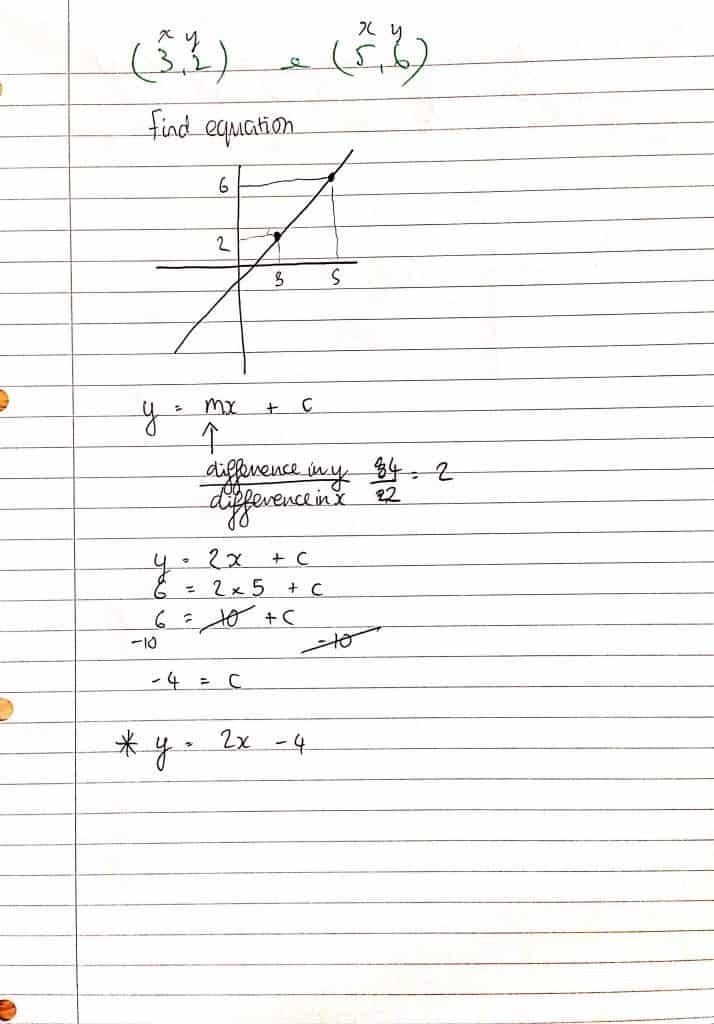


Leave a Reply