Solving inequalities really do crop up in real life – it’s just a mathematical way of describing something…
This series of 3 minute math is designed as a quick reminder for some of the main topics. I hope they help to provide a focus and a way forward. If you need any more detail please search the site or contact me – always pleased to answer any questions!
All the very best with your studies.
Where are inequalities used?
In other words you have to be older than, or equal to, 17 to drive.
Inequalities can get a little more complicated and, at GCSE, tend to be given with two variables. As an example, lets say that you had £60 to spend and wanted to buy some T shirts (£3 each) and jeans (£17 each).
Let x be the number of T shirts and y be the number of jeans. The amount of money to be spent is less than or equal to £60. The equation would look like this:
Transcript from the video:
“Welcome to 3 Minute Maths. This is all about solving inequalities. There are a couple different types of questions you’re going to get. Generally speaking, they tend to be fairly high level, A* types of questions, GCSE or equivalent.
You might get a question that’ll look something like this: . That’s a typical one mark or two mark question that you can treat in the same way as a linear equation. What we do is work out that the value of x is less than or equal to 12 by adding 3 to both sides – that will give us the ability to put x on one side all on its own.
– 3 + 3 is 0 so that’s going to mean we get , which is
. That would be the answer to this question.
Now, the only type of ‘curveball’ they can throw is where they put in a fraction. So you get something which is like this: . That’s an A* type of question. Typically, this would be two marks, but we would treat it in much the same way as we would with any other linear-type equation.
To start, I’m going to multiply both sides by 3 because then I can get rid of the denominator and get 2x left on its own. It was but the 3’s cancel each other out. Then, on the other side of the inequality, I got 10 x 3, which is:
Well, means that to get the value of x itself, I divide both sides by 2. I got to get x on its own so I get
.
And, those are really the only two types of questions that you’re going to get for solving inequalities. If you carry on watching the videos, we’ll have a look at more sophisticated versions of this. I hope you’ve found this useful and I’ll look forward to seeing you inside the next three minutes.”
Watch the video on YouTube Solving Inequalities as a Linear Equation
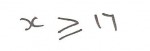
closed includes open doesnt
so if its -4 -3 -2 -1 0 1 2 3 4 open both ends from minus 3 to 3 for
solution if closed includes minus 4 is that right