How to work with probability tree diagrams

Probability tree diagrams are just a picture that show all the possible outcomes, from a series of events. They can be quite useful, but probability needs some careful thought.

Watch the video and download the quick test – good luck!

This video deals with a GCSE question:

There are 3 strawberry yoghurts and 4 peach yoghurts in a fridge. Kate takes a yoghurt at random from the fridge. She eats the yoghurt. She then takes a second yoghurt at random from the fridge. Work out the probability that both yoghurts are the same flavour.

Another example:

Lauren takes the bus to school but, unfortunately, she misses the bus 1/3 of the time. If Lauren misses the bus she has to walk to school, and 80% of the time is late. If Lauren catches the bus, she in late for school 25% of the time.

Calculate the probability that Lauren misses the bus AND is late for school.

There are a couple of things to consider:

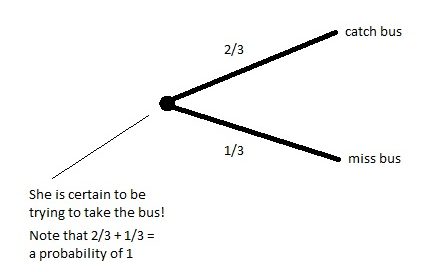
• Firstly, she is certain to be trying to take a bus. This means that there is a probability of 1, represented by a dot, on a probability tree
• She might catch, or miss, the bus

So the first part of a probability tree will look something like this:

2/3 of the time she catches and 1/3 of the time she misses. The 2/3 and 1/3 must add up to 1 as she is certain to be trying!

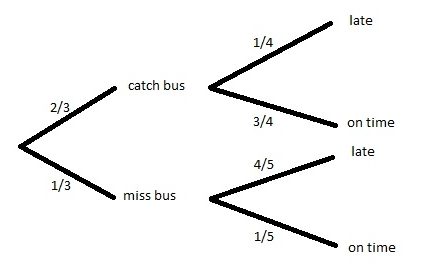
The next part of the probability tree deals with the next event:

• For this type of question, it’s usually better to convert the percentages to fractions
• If Lauren catches the bus 3/4 of the time she’ll get to school before the bell, 1/4 of the time she’ll be late.
• Likewise, if Lauren misses the bus, and has to walk, 4 out of 5 times she’ll be late. 1/5 time she’ll make it.

Putting all this together a complete probability tree diagram will look something like this:

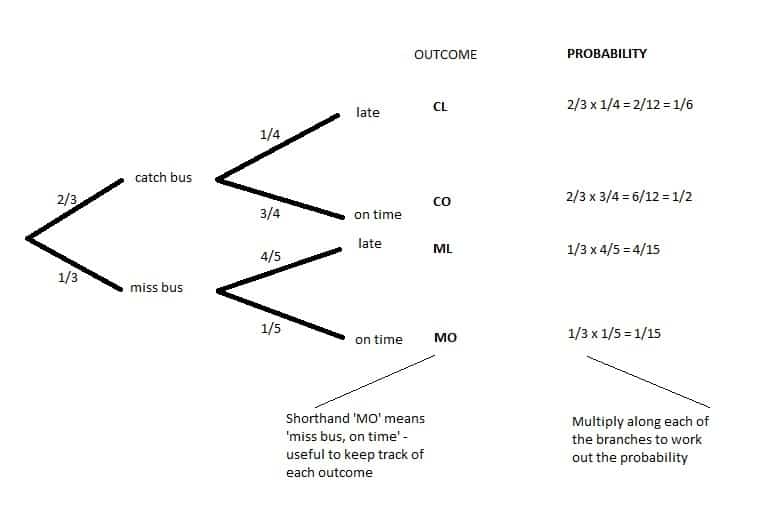
OK … so now lets look at ‘outcomes’ .. meaning the probability of an event happening. We multiply along the branches to work out the probability of each outcome.

Adding the different outcomes to each of the branches, Lauren’s probability tree should look something like this:

So the probability that Lauren misses the bus AND is late for school – outcome ML –  is:

1/3 x 4/5 = 4/15

In other words for every 15 journeys Lauren will miss the bus and be late 4 times.

Click here for Quick Test Probability Tree Diagrams practice questions.